Distância entre primos gêmeos que possuem algarismos da unidade iguais

Primos Gêmeos são todos os pares de números primos cuja distância entre eles é de duas unidades, como por exemplo os pares: $(3,5)$, $(5,7)$ e $(11,13)$. Se observarmos os pares de primos gêmeos terminados com os mesmos algarismos das unidades, podemos notar uma regularidade.

A cada par de primos gêmeos, que detém a característica de possuir os algarismos das unidades iguais, a distância para o próximo par com a mesma característica é sempre de $30k$, com $k$ inteiro, com exceção para os pares $(3,5)$ e $(5,7)$, pois não possuem primos terminados nas mesmas unidades, por serem múltiplos de $5$.

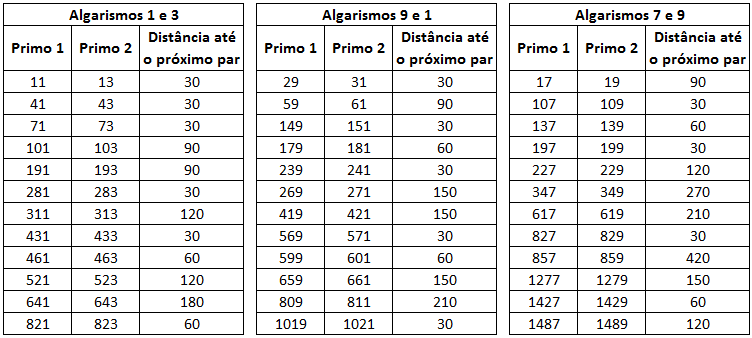
Para ilustrar alguns pares de primos gêmeos com estas características, montamos a tabela abaixo onde podemos observar a distância entre os pares.

Teorema:

A distância entre todos os primos gêmeos com algarismos das unidade iguais é, para um certo $k$, de $30k$, com $k \in \mathbb{Z}$, com exceção aos pares $(3,5)$ e $(5,7)$.

Demonstração:

Esta demonstração foi elaborada pelo professor Eduardo Wagner, do IMPA. Sejam dois pares de primos gêmeos:

$$\begin{equation*} (x-1, x+1) \quad \text{e} \quad (y-1,y+1) \end{equation*}$$

Se os algarismos das unidades dos primeiros elementos de cada par são iguais, então:

$$\begin{equation*} (y-1)-(x-1)=10k \end{equation*}$$

Ou seja, $y-x=10k$, com $k$, inteiro.

Por outro lado, sabendo-se que entre três números consecutivos há sempre um que é divisível por $3$, podemos então inferir que $x$ e $y$ devem ser obrigatoriamente múltiplos de $3$, pois, se $x$ não for múltiplo de $3$, então $x-1$ ou $x+1$ será, o que não pode ser, pois eles são primos.

Então a diferença
$$\begin{equation*} (y-1)-(x-1)=x-y \end{equation*}$$

é múltipla de $3$, ou seja, a diferença $x-y$ é múltipla de $30$.

Este artigo e teorema foi elaborado por Luiz Carlos Pitzer, mestrando do Profmat e especialista em metodologia de ensino de Matemática.

Contato: luizpitzer@gmail.com.

Links para o artigo:

• http://bit.ly/Distancia-Primos-Gemeos
• https://www.obaricentrodamente.com/2018/02/distancia-entre-primos-gemeos-com-algarismos-das-unidades-iguais.html

Veja mais:

• Sobre os primos gêmeos
• Construindo uma sequência de números não-primos
• A demonstração de Euclides sobre a existência de infinito números primos